一、什么是机器学习

　　（一）

• 对于给定的任务T，在合理的性能度量方案P的前提之下，某计算机程序可以自主学习任务T的经验E；随着提供合适、优质、大量的经验E，该程序对于任务T的性能逐步提高。
• 机器学习是人工智能的一个分支。我们使用计算机设计一个系统，使他能够根据提供的训练数据按照一定的方式来学习；随着训练次数的增加，该系统可以在性能上不断学习和改进；通过参数优化的学习模型，能够用于预测相关问题的输出。

　　（二）这里最重要的是机器学习的对象：

• 任务Task，T，一个或者多个
• 经验Experience，E
• 性能Performance，P

　　即随着任务的不断执行，经验的积累回来带来计算性能的提升

二、机器学习的分类

• 有监督学习
• 无监督学习
• 增强学习

三、机器学习的内涵和外延

　　给定数据的预测问题

• 数据清洗/特征选择
• 确定算法模型/参数优化
• 结果预测

　　不能解决

• 大数据存储/并行计算
• 做一个机器人

 

 

 

 三、机器学习的一般流程

　　数据收集--》数据清洗--》特征工程--》数据建模

 四、导数

• 简单来说，导数就是曲线的斜率，是曲线变化快慢的反应
• 二阶导数是斜率变化快慢的反应，表征曲线凸凹性

　　（1）二阶导数连续的曲线，往往称之为“光顺的”

　　（2）加速度的方向总是指向轨迹曲线凹的一侧

• 　Taylor公式-Maclaurim公式

 

 

•  方向导数

　　如果函数z=f(x,y)在点P(x,y)是可微分的，那么，函数在该点沿着任一方向L的方向导数都存在，且有：

　　

　　其中，Ψ是x轴到方向L的转角。

• 梯度

　　设函数z=f(x,y)在平面区域D内具有一阶连续偏导数，则对于每一个点P(x,y)€D，向量

　　

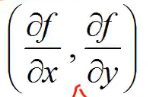
　　为函数z=f(x,y)在P点的梯度，记作gradf(x,y)

　　梯度的方向是函数在该点变化最快的方向

• 

　　

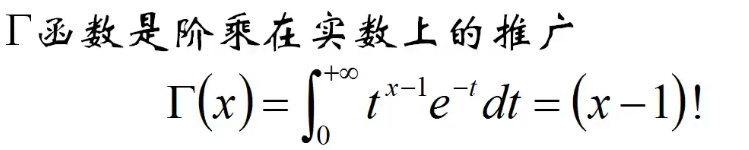
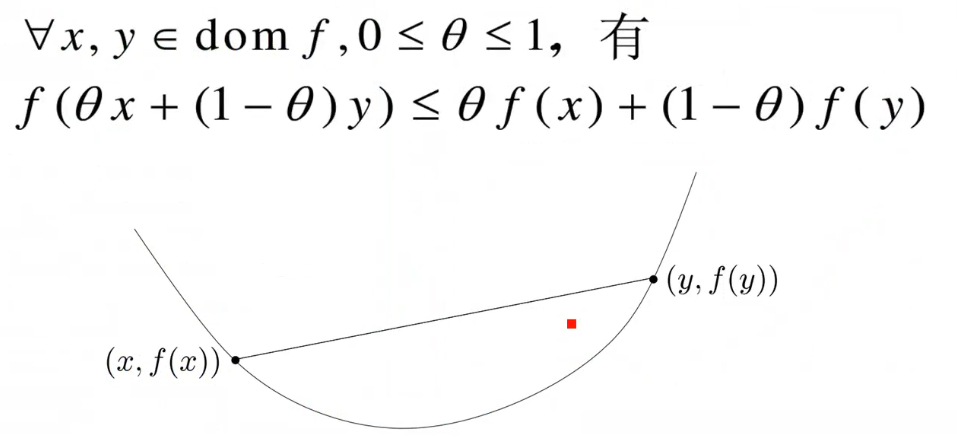
• 凸函数

　　若函数f的定义域dmof为凸集，且满足

　　

　　

  

资料来源：小象学院  邹博   仅供学习研究